最大公因數的概念

 與最大公因數最相關的概念應該是分數的約分，

於是我打算從這部分切入：

《例1》    6/□            8/□     其中□填入的數字原則須為質數而且6/□ 8/□ 必須為正整數，於是：

                    6/2            8/2

            =》  3/□           4/□     □不能再填入任何數

∴(6，8)=2

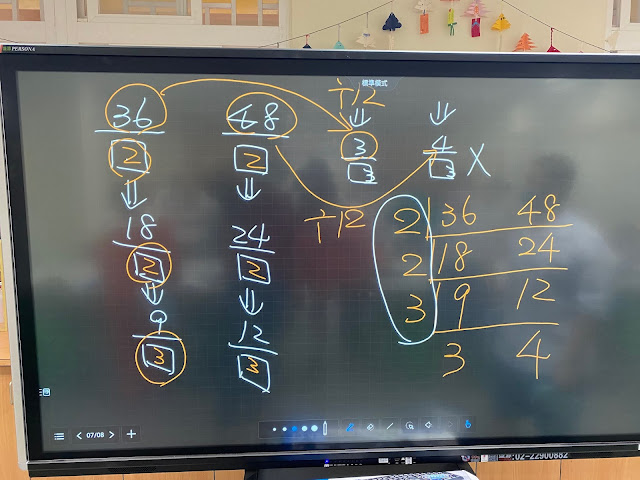
《例2》    24/□            36/□

          =》 24/2            36/2

          =》 12/□            18/□

          =》 12/2            18/2

          =》  6/□              9/□

          =》  6/3              9/3

          =》  2/□              3/□   □不能再填入任何數

∴(6，8)=2×2×3

此時與短除法的算法對照一下：

             2｜24     36

             2｜12     18

             3｜  6      9

                     2      3

是不是覺得跟上面的約分過程很像呢?

《例3》    595/□            2431/□

              此時你會發現，無從下手，因為沒有很顯而易見的約分數字出現，所以這時候只能借用標準分解式的方法來處理，因為如果是最大公因數，那麼這個數一定會都是595跟2431兩數的因數。

595會比2431好分解，因為一定是5的倍數，於是：

595=5×119=5×7×17

所以檢查：2431是否能被7或17整除?

2431=17×143=17×11×13

於是：會發現595跟2431可以被17整除，而且再也沒有其他的數可以約分了，所以：

(595，2431)=17

根據例3的例子，我們就發現：原來我們可以用

標準分解式來找最大公因數。

《例4》找 2^2×3×5^2、2^3×3^2×5^3的最大公因數：

                2^2×3×5^2/□     2^3×3^2×5^3/□

          =》 2^2×3×5^2/2    2^3×3^2×5^3/2

          =》 2×3×5^2/□        2^2×3^2×5^3/□

          =》 2×3×5^2/2        2^2×3^2×5^3/2

          =》 3×5^2/□            2×3^2×5^3/□

          =》 3×5^2/3            2×3^2×5^3/3

          =》 5^2/□                2×3×5^3/□ 

          =》 5^2/5                2×3×5^3/5   

          =》 5/□                   2×3×5^2/□

          =》 5/5                   2×3×5^2/5 

          =》 1/□                   2×3×5/□

                □不能再填入任何數

於是：最大公因數=2×2×3×5×5=2^2×3×5^2

如果每題都這樣算，應該會瘋了，所以可以觀察一下簡單的方式：

2^2×3×5^2=》有2個2、1個3及2個5可以拿來約  

                         分

2^3×3^2×5^3=》有3個2、2個3及3個5可以拿來

                            約分

所以取共同可以約分的部分：

2個2、1個3及2個5

於是最大公因數為2^2×3×5^2

1

2

3

4

5

6

7