平行公設、三角形內角和、全等及尺規作圖

 這次教八年級的全等與尺規作圖這部分，決定來點不一樣的切入點：

第一部份：

先從平行教起，帶出同位角及內錯角概念，透過平行狀態下來推出內錯角相等的概念，然後再應用來教授三角形內角和180度的內容(因為內角和180度與平行公設是等價概念)不用像課本是用摺紙概念來模糊帶過，畢竟摺紙會產生誤差之狀況發生(感謝俊儀教授的內外角測量軟體，讓學生感覺到測量會出現179度或181度的狀況)。

第二部份：

先處理三角形的全等，再回頭處理尺規作圖---

會考的尺規作圖都不是在考尺規作圖，而是在判別作圖利用到的幾何原理的正確與否，於是乎利用了2-3節課的時間重拾久久未用的簡報(因為怕弄太多的雜訊進去)製作全等的內容，然後一步步地把我想呈現的全等概念一頁一頁慢慢地呈現，並在上課的過程中發現

整個的思考脈絡有所偏差，故中途又重新編來了一次簡報內容的順序，後來在使用時，就很順暢了。尺規作圖的內容還沒開始上課，待續....

全等的脈絡：

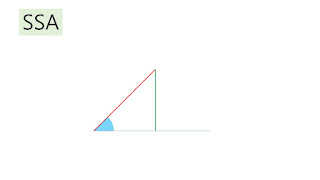
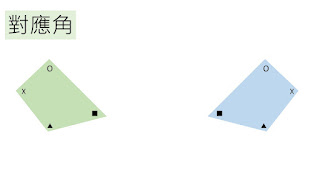
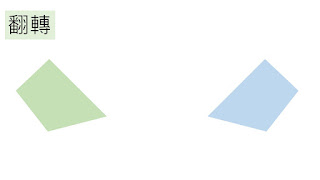
全等條件是要由少至多呢，還是由多至少呢？前者似乎比較容易處理，條件由一個的A或S，擴增到兩個條件的SS、SA、AA，再擴增到三個條件的SSS、SAS、AAA、ASA、AAS、SSA(這是我思考過後個人覺得最佳的上課順序)，並從SSA中去帶出所謂的RHS全等(學生比較能接受SS90°的講法，因為直接連結直角三角形，這也要感謝俊儀教授的新法共備數的共備課程)，最後得到全等性質就是可以分成兩大類(SSS及ASA)。

P.S.很多內容在處理時也應用到彰師大生根教材內容的薰陶，感謝彰師大CA教授前幾年認真帶我們這群夥伴講解有關課本內容的利弊，及應該要注意的相關細節，沒有這幾年的養分供給，應該不會有現在成長長大的我!!!